‘Data’ in the Royal Society’s Philosophical Transactions, 1665–1886

Introduction

In an era of big data and data intensive science which, as some have suggested, may even make models, theories and hypotheses obsolete, it can be difficult to imagine that notions of data were not always already central to scientific practice.¹

How did the notion of ‘data’ come to be such a core part of thinking about science? While scholars have studied the histories of various epistemic units, including facts, experience, observation and, more recently, information, surprisingly little is known about the history of the notion of data.² The notion is often taken for granted, used as a familiar idea to explain other developments.

This paper contributes to understanding the history of the concept of data by studying a specific development before the current data revolution, in the Philosophical Transactions of the Royal Society of London. Its first issue came out on 6 March 1665. How did the concept of data function in the Royal Society’s journal? Here I will show that the notion of data got introduced in an early technical usage through the field of mathematics (and, to a certain extent, astronomy) as indicating given quantities in geometrical problem solving. From there, it expanded and gained prominence in other fields, including Earth science, physics and chemistry. I suggest that throughout the period covered, the notion retains an associated epistemic structure, generalizing the function that can originally be found in its use in mathematics.

The next section presents how data figures in the Philosophical Transactions, paying attention to technical usage of the term. The following two sections respectively chart how uses of the notion of data vary by field of publication, and distinguish three functions of data that occur across different fields (data in computation, as information and in relation to theory). The final section places these findings in a wider framework by identifying an epistemic structure associated with the notion that stays relatively stable over the course of two centuries. I conclude that ‘data’ in the Society’s journal is not a merely rhetorical category, nor can it be used interchangeably with ‘evidence’.

A note on methodology. In this study I will draw on linguistic evidence regarding how the term ‘data’ is used. Such an approach is not uncontroversial, given that terms, as lexical items, are not identical to concepts (or notions, ideas), which relate to cognition. Several terms may connote the same idea. For instance, ‘home’ and ‘house’ may both connote a dwelling for human habitation. Conversely, a single term may pick out different concepts, as is the case with polysemy. ‘Crane’ may connote either a bird or a piece of construction equipment, depending on the context. That said, linguistic evidence can be a guide in the study of the history of concepts, especially if measures are taken to mitigate any potential limitations. Irrelevant uses of a term can be sifted out either manually or through automated methods. In the current investigation I do this early on by distinguishing in the next section three ways in which the term ‘data’ occurs in the corpus studied and concentrating the inquiry on only one of those ways. Further, one can identify adjacent terms that connote the concept at issue. Here I make a start with this work for the concept of data in mathematics and the empirical sciences.

Data in the Philosophical Transactions corpus

The focus here will be on publications from the journal’s inception in 1665 up to and including 1886, after which it split into two separate journals, one for mathematics and physics (A: Mathematical, Physical and Engineering Sciences) and the other for life sciences (B: Biological Sciences). The entire corpus of this period contains 7812 distinct published items.³ The contributions vary significantly in length and purpose. They range from half-page book excerpts, letters and book reviews to formal articles and treatises stretching to hundreds of pages.

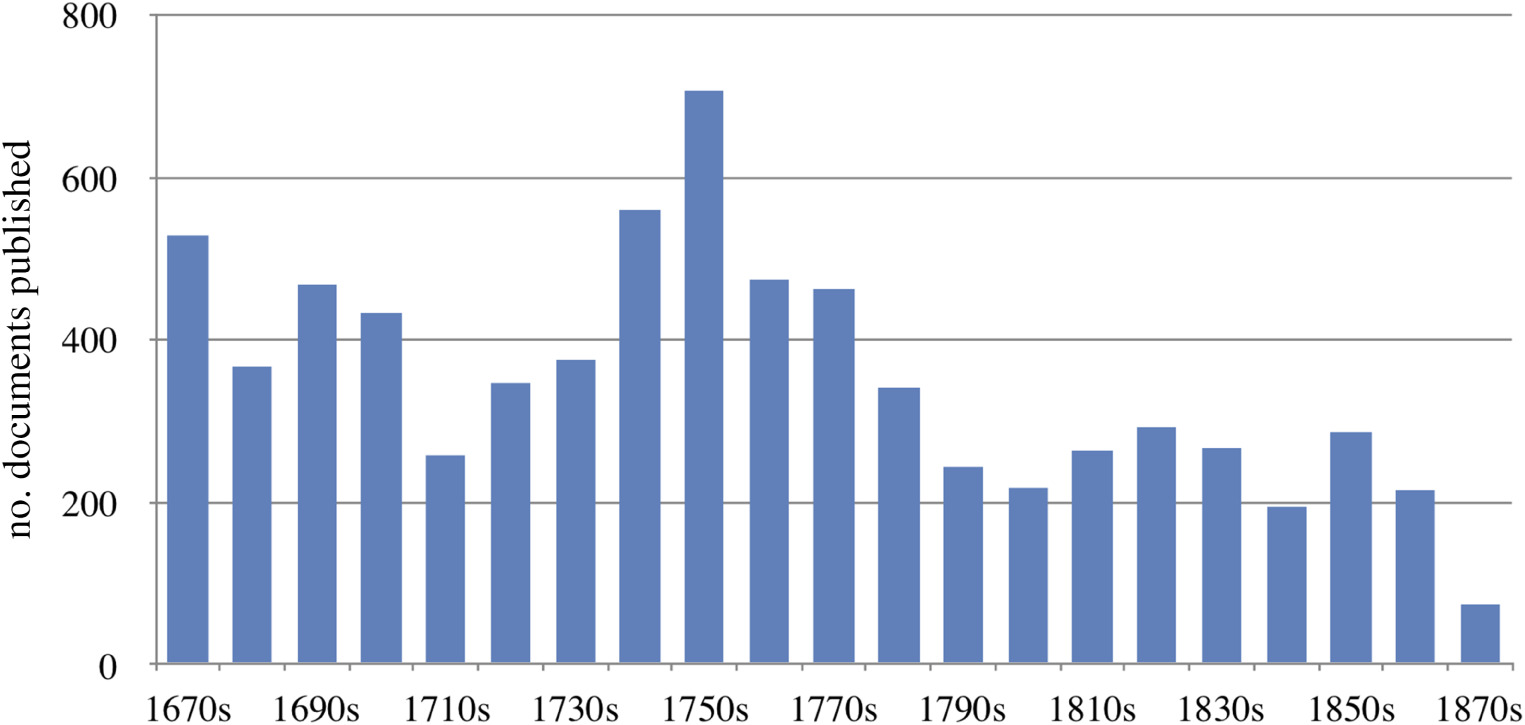
The total number of publications in the journal initially reaches a peak of 708 published items (or roughly 71 per year) during the 1750s, and decreases thereafter (figure 1). This fall coincides with the Royal Society formally taking over the financial and editorial management of the journal in 1752, establishing a Committee of Papers which selected papers for publication.4 (The journal adopted a form of formal peer review only in 1832, which, incidentally, coincides with another slight dent in the number of published items.) The fall in the number of publications persists during the later eighteenth and most of the nineteenth century. However, perhaps surprisingly, during this time the amount of information contained in each individual document actually goes up, more than tripling between the 1800s and 1880s (figure 2). As a result, the total information quantity published by the journal continues to increase well into the nineteenth century.

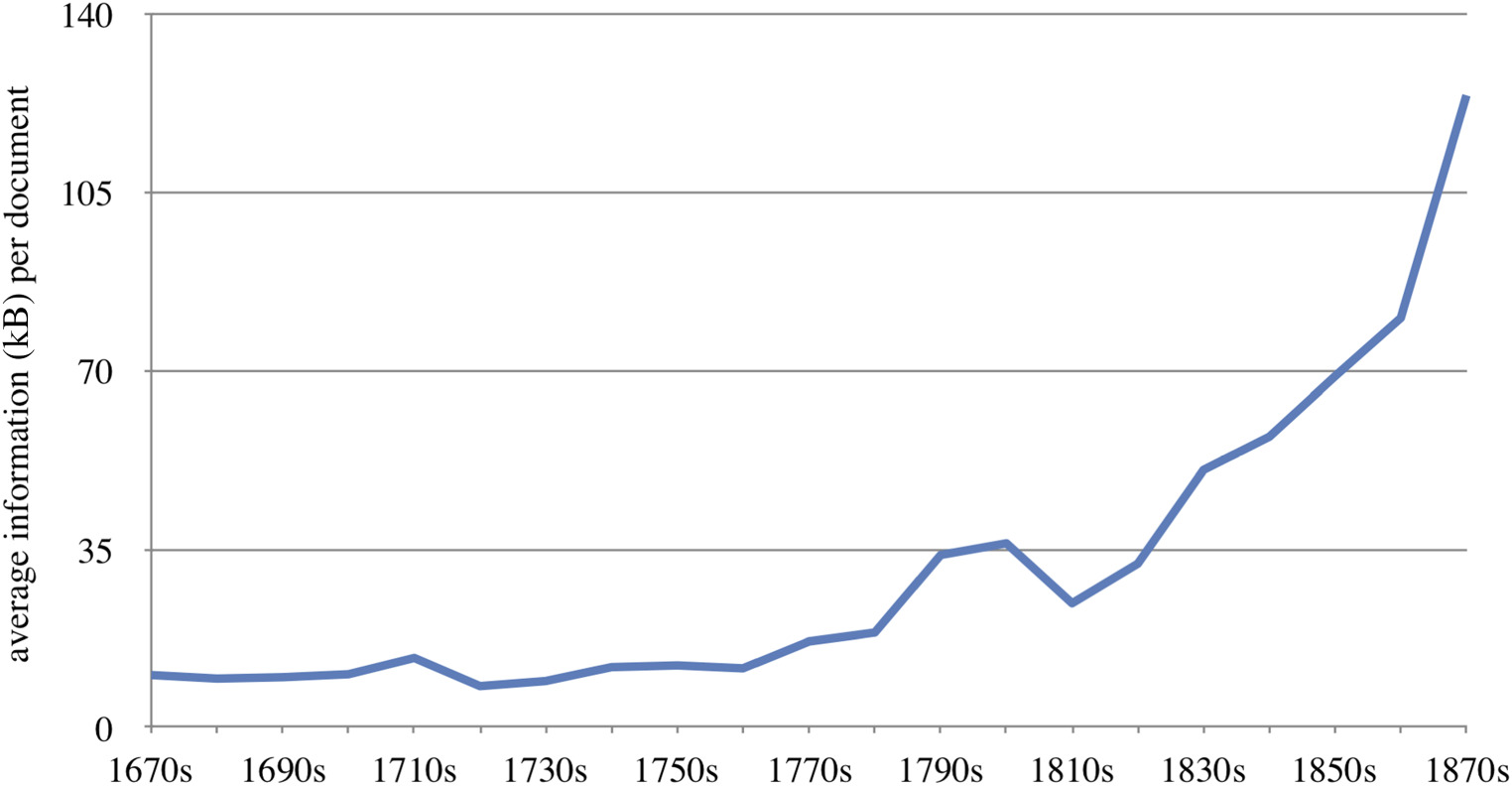
Information quantity per published item is measured in kilobytes (kB) based on .txt files created from document content extracted from optical character recognition- (OCR)-processed PDF files.

Documents were consulted as OCR-processed PDF files using the ATLAS.ti software for qualitative data analysis. A full-text search for ‘dat*’, after checking for OCR errors, turned up 1826 occurrences in total of ‘data’ (including grammatical variants such as ‘datae’, ‘of the given’) in 753 separate documents, which amounts to only 9.63% of the total corpus. For comparison, during the same period, terms such as ‘observation’ (hits in 3632 documents, or 46.49% of the total), ‘fact’ (1878 hits, or 24.03%), ‘measurement’ (1525, or 19.52%), and even ‘phenomena’ (phaenomena) (1255, or 16.06%) are more common. Figure 3 shows the distribution of those absolute occurrences over time, suggesting that use of ‘data’ is already substantial in the late seventeenth century.

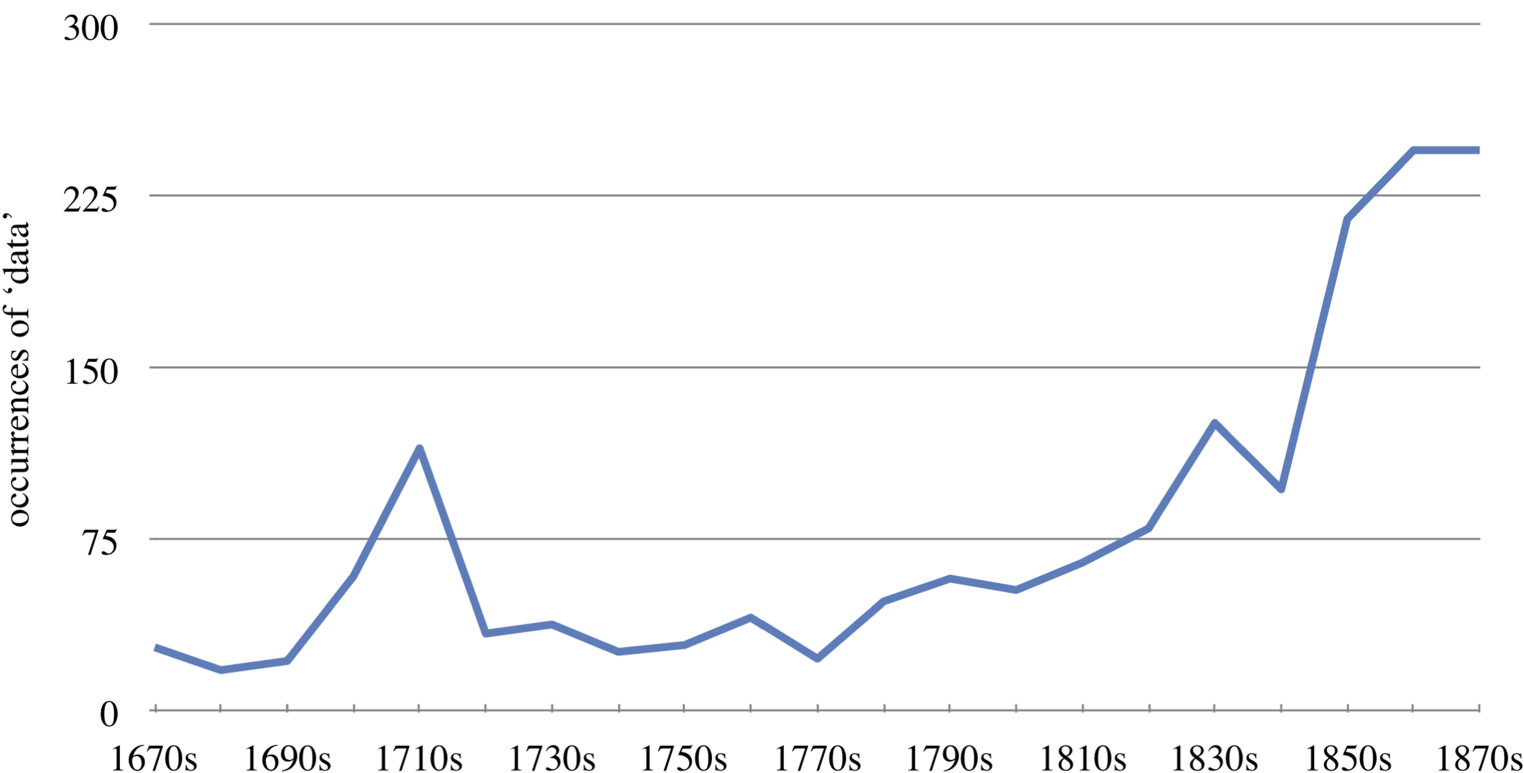
Using a full-text search of OCR-processed PDFs has its limitations, in that one’s results will be restricted by the quality of the OCR processing. OCR is generally optimized for modern type, but does not always perform as well with older typefaces (or handwriting, for that matter). Given this limitation, occurrences of ‘data’ in the earliest articles may still be under-reported.

Within these 1826 occurrences of ‘data’, it becomes possible to identify specific usages. Uses of ‘data’ can be distinguished as falling into three main categories: (I) ‘data’ used to identify dates (meta-data); (II) ‘data’ in adjectival form; (III) ‘data’ used as a substantive. Working with this distinction, I found 44 of the hits for ‘data’ in this corpus in Latin as temporal indicator, for example on a letter ‘data 30 Julii 1697’ (‘dated 30 July 1697’). These I will not look into much further, because their formulaic character makes them of little interest for a prehistory of a philosophical notion of ‘data’. Another, slightly larger, category includes 386 cases (21.13% of all hits) where ‘data’ occurs in a past participle form used adjectivally to indicate that something has been given. Consider, for example: ‘data area’ (‘a given area’) or ‘data differentia terminorum’ (‘a given difference of terms’). Here, an area or a difference of terms has been given in a certain (problem-solving) context.

Occurrences of ‘data’ falling into categories (I) and (II) occur in papers written in Latin or in English papers incorporating Latin phrases. As the language of communication rapidly shifts to English, these do not comprise the majority of the papers. Nonetheless I think it is important to identify these categories from a viewpoint of completeness, given that they are among the results found when one searches for ‘data’ in the Philosophical Transactions corpus.

The remaining group, which is also the largest, involves 1396 cases (76.45% of the total number of hits) of ‘data’ used as a substantive, distributed over 573 distinct documents. For instance in a 1669 document, Plymouth-based physician William Darston refers to ‘the Data of the Circulation of the Blood’5 that did not yet enable him to form a diagnosis about a particular patient. In a different document, an author notes that ‘we should then have had data to decide’,6 in short that data is required for decision making.

These observations are consistent with what is known about the linguistic history of ‘data’ in English more generally. Etymologically, the Latin term ‘data’ is a plural participle form of the verb ‘dō’, ‘to give’, translating roughly ‘givens’ (singular neuter past participle: ‘datum’, ‘given’). As a form of such an everyday word, the term ‘data’ is everywhere in classical and neo-Latin. However, over time some more technical usages other than designating everyday instances of giving do emerge. One of these occurrences is where ‘data’ indicates a date mark (e.g. of a letter written)—what Furner calls ‘data as meta-data’—and which can already be found from around first century BCE onwards.7 Another is a substantive (nominal) usage, where a ‘datum’ is ‘A thing given, a gift delivered or sent’,8 which arises from the late sixteenth century. From the early seventeenth century onward, ‘data’ gets used to refer to records of numerical information.9 It has been argued that while the term ‘data’ was naturalized in the eighteenth century, even in the nineteenth century it remained a fringe term which played only a minor role in many debates.10

Focusing now on the use of ‘data’ as a noun (setting aside the meta-data and adjectival uses) reveals that this substantive usage of ‘data’ gets a foothold only somewhat later in the journal’s records (in the early eighteenth century), and moreover forms the bulk of all subsequent occurrences of data, as shown in figure 4. Use of ‘data’ as a substantive solidifies only markedly later than verbal or meta-data uses, that is, not since the 1680s but only in the 1720s. It is plausible, though wider linguistic evidence would have to bear this out, that the more technical use of ‘data’ as a substantive develops out of the use of ‘data’ in participle form.

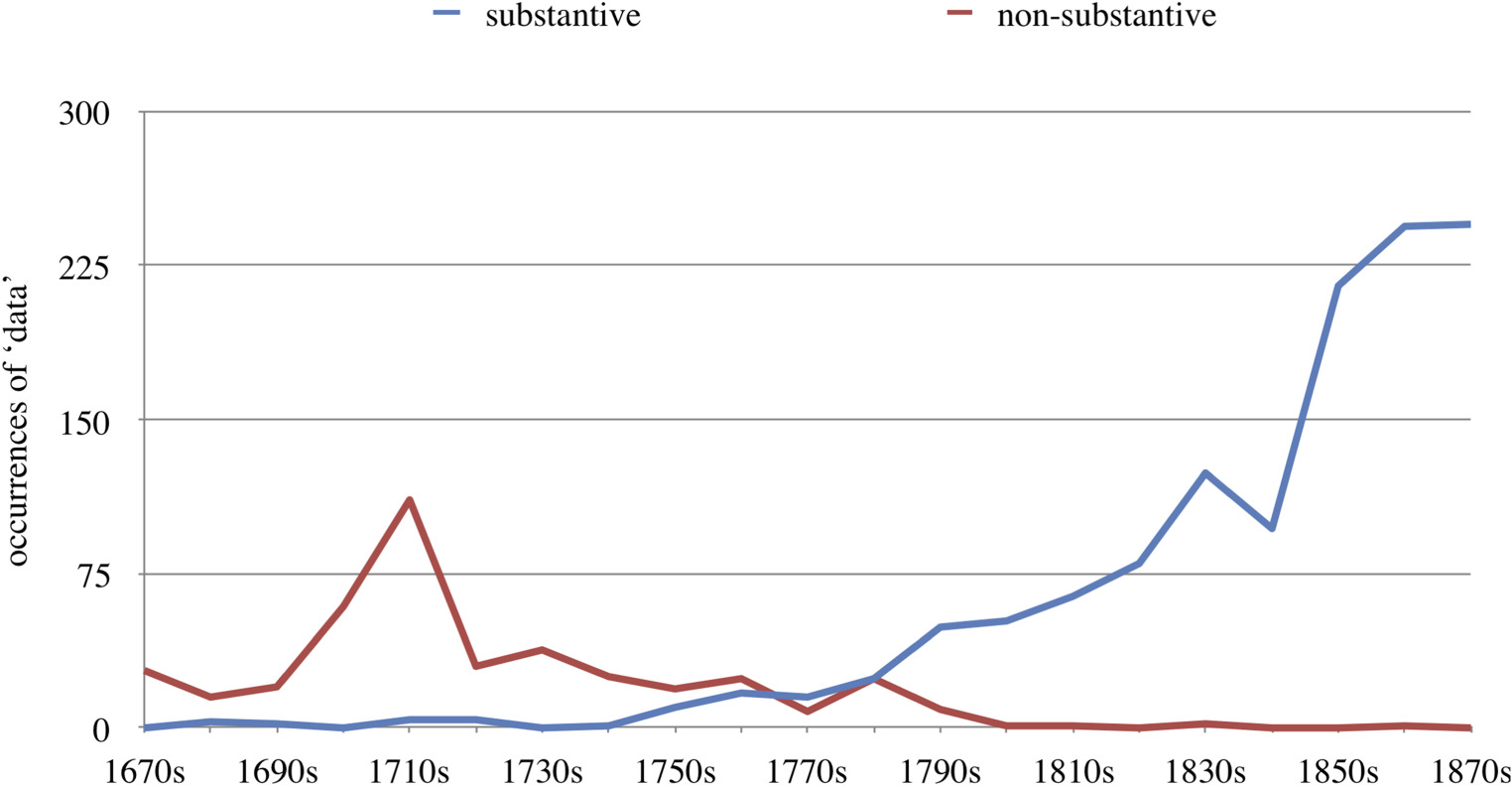
Could the increase in occurrences of ‘data’ as a substantive in the Philosophical Transactions simply be the result of the journal’s larger output in terms of quantity of information? If more information is being published, then there is more content in which the term ‘data’ might occur. Indeed, both total information quantity and occurrences of ‘data’ by and large increase from the middle of the eighteenth century onward. However, when considering specific developments per decade, changes in the number of occurrences of ‘data’ turn out not strictly to correlate with an increase or decrease of total quantity of information published. Focusing on the period 1750–1879—from the beginning of this joint rise to the end of the last full decade studied here—it turns out to be actually slightly more likely for a change in the number of occurrences of ‘data’ to move in a direction opposite to a change in the total quantity of information, than for those changes to line up. That is to say, in seven of the 13 decades covered here (namely, the 1760–80s, 1800–10s and 1860–70s), occurrences of ‘data’ were up, while the total amount of information published was down, or vice versa. This suggests that the increase in such occurrences of ‘data’ cannot be explained simply as a result of an increase in the quantity of information that got published. Instead, there must be an actual change in the published material.

A further differentiation can be made by looking at how occurrences of ‘data’ distribute across different philosophical and scientific fields. To bring this into view, I hand-coded all 1826 hits for the term ‘data’ individually for areas based on context, using common categories of scientific disciplines. By far the most prominent field in which ‘data’ is used as a term is within the area of physics (including engineering) with 435 cases (or 24.07% of the total), followed by Earth sciences (including geology and meteorology) with 404 cases (22.36%), chemistry with 297 cases (16.44%), mathematics (including statistics and probability theory) with 266 cases (14.72%), astronomy (168 hits, 9.30%) and biology (147 hits, 8.14%). The remaining categories, which include domains such as metrology, agriculture, medical science, history, anthropology and logic, each scored fewer than 100 occurrences.

Before considering any developments over time, it will be helpful to grasp the broader landscape of scientific fields covered on the pages of the journal. To bring this into view, I used the DARIAH Topics Explorer to produce a topic model for the full collection of documents (all 7812 items) published in the Philosophical Transactions. For each of the four quarters of the publication (Q1: 1665–1720; Q2: 1721–1775; Q3: 1776–1830; Q4: 1831–1886), I produced 100 topics (or ‘bags of words’; that is, clusters of words that are neither really common—such as ‘the’, ‘is’, ‘it’—nor extremely rare, and that are likely to occur near one another). These topics were manually coded as indicating a topic belonging to one of the most prominent six fields published in the Transactions, namely: mathematics, astronomy, physics, chemistry, Earth sciences and biology. For example, a topic that included words such as ‘blood’, ‘heart’, ‘pulse’, ‘death’ and ‘normal’, I classified as belonging to biology; a topic with words including ‘electricity’, ‘force’, ‘power’, ‘experiment’ and ‘influence’, I coded as belonging to physics; while ‘feet’, ‘glacier’, ‘ice’, ‘valleys’ and ‘lower’ were classified as belonging to Earth sciences. Publications in the much smaller fields, such as archaeology, as well as general topics (for example with word clusters such as ‘curious’, ‘particular’, ‘making’, ‘mention’d’, and ‘discourse’) I coded as ‘other’. The same holds for when the cluster of words within a topic was too mixed to classify as belonging primarily to one field.

The resulting overview of the relative prominence (rather than absolute number of articles) of scientific fields in the journal is shown in figure 5. Noteworthy is that topics in biology and Earth sciences are comparatively prominent in Q1 and Q2. They remain well represented in Q3; more strongly, topics in Earth sciences are at their most prominent during that quarter. But Q3 also sees the relative growth of topics in physics and chemistry. In the final quarter, physics and chemistry continue to gain relative prominence, while topics in mathematics also come somewhat more to the fore. By contrast, topics in astronomy, which had a reasonable presence in Q2, become relatively more obscure in Q4.

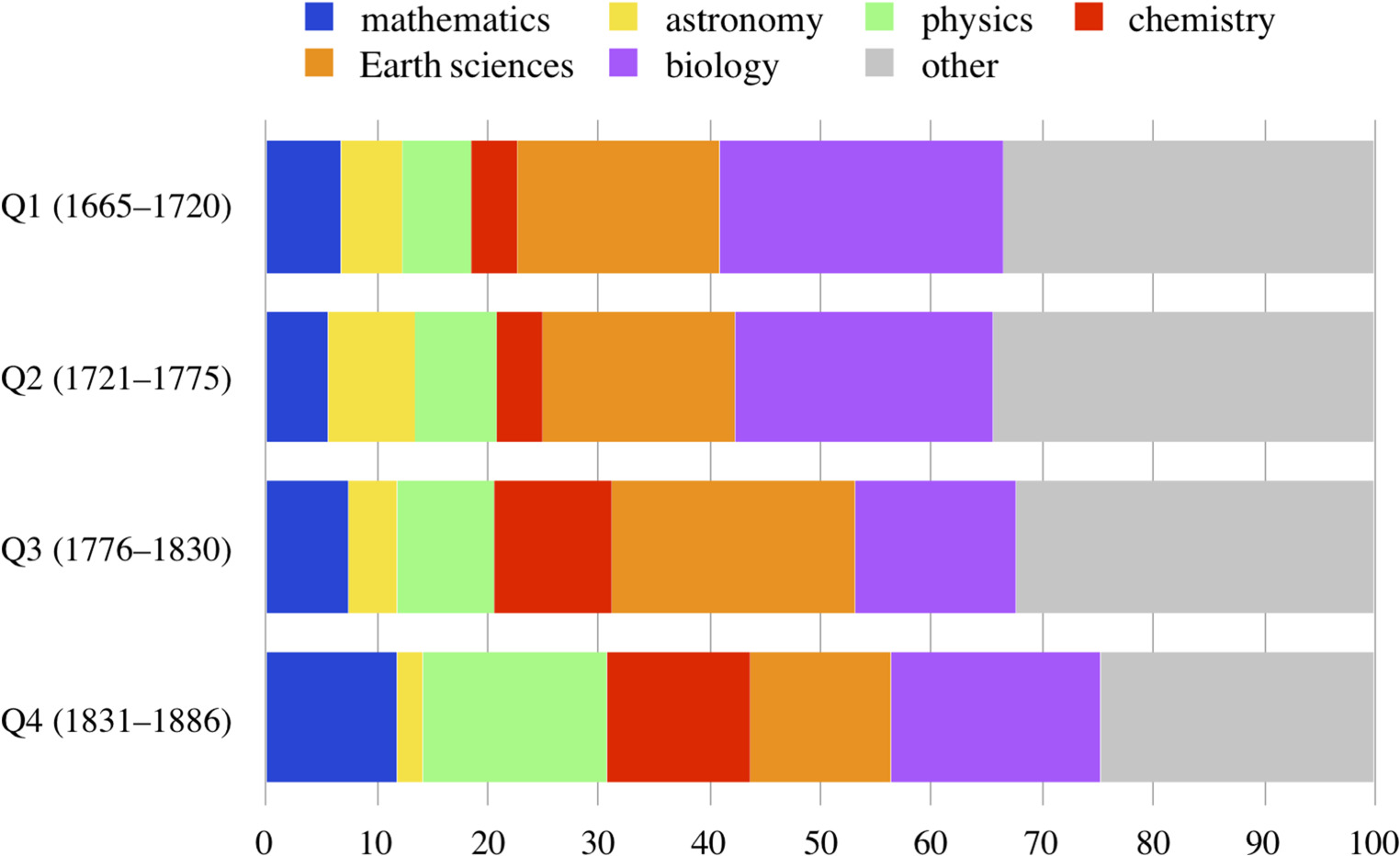
This broader context yields significant insights. As noted, the term ‘data’ is most frequently used in physics. However, topics in physics are at no point most prominent among work published in the Transactions. Likewise, in three out of four quarters studied here, topics in biology appear to be comparatively most prominent, but the term ‘data’ is nonetheless little used in this field. Hence, how frequently the term ‘data’ is used does not obviously correlate with the relative prominence of the scientific field in which it occurs. Authors publishing in physics are comparatively more prone to refer to ‘data’ than those in biology.

Let me now turn to any significant trends in uses of ‘data’ within these several scientific domains by looking at developments over time, zooming in on key features of talk of ‘data’ within the first and final quarters of the Philosophical Transactions’ publication span in the period 1665–1886. Such an inquiry can bring into sharper view how an initially almost negligible usage in the seventeenth century became more prominent and spread out into different fields by the end of the nineteenth century.

From mathematical given to empirical observations

‘Data’ enters the Philosophical Transactions corpus through the field of mathematics. Turning to developments in the first quarter (1665–1720) of the years of publication studied here gives some indication of how this works. In the first quarter the Transactions publish a total of 2395 documents. Within these documents, there are 252 occurrences of ‘data’, distributed over only 99 documents (or hits in only 4.13% of the total number of documents in Q1). Of these, the majority (65 cases) are Latin documents which use ‘data’ as a participle.

Considering different scientific fields, I found that by far the largest portion (151 hits, 59.92%) occurs in the area of mathematics, followed by physics (44 hits, 17.46%) and astronomy (33 hits, 13.09%). For example, within mathematical works one can find reference to ‘a given proportion’ (datâ proportione), ‘given points’ (data puncta), ‘given positions A D B’ (positione data A D B), ‘a given ratio of refraction’ (data Ratione Refractionis) or ‘any given parabola’ (data quavis parabola). This talk of data occurs within the context of mathematical problem solving. The points, lines and ratios are given, in that they form the basis upon which other things—more points, lines, ratios—can be found or established. In general, in these cases the term indicates a structure in which one quantity is held fixed such that another can be determined.

The prominence of mathematics (especially geometry) within the Philosophical Transactions corpus makes sense in light of the early modern reception of Euclid’s work Data (Gr. Dedomena, Δɛδομένα), which in editions of the time was often appended to publications of his Elements. In Data Euclid deals with the solution of geometrical problems by analysis of things already known or ‘given’; ‘data’ in this context are those quantities that are already known in a particular mathematical problem and that contrast with the quantities sought, or the quaesita. This technical usage sometimes carries even beyond the Latin, also on the pages of the Philosophical Transactions. For example, in a text on probability posthumously published in the journal, Thomas Bayes writes ‘Given the number of times in which an unknown event has happened and failed: Required the chance that the probability of its happening in a Angle trial lies somewhere between any two degrees of probability that can be named’⁴, which exactly mirrors the traditional Euclidian use. Further, some authors switch flexibly back-and-forth between ‘data’ and ‘given’, for instance when Thomas Barker writes of determining the path of a comet: ‘Then the other data being already known, and one place given, its whole course may be traced.’⁵

This mathematical context remains in early accounts of data, for example in John Harris’s Lexicon Technicum (1725). Here ‘data’ are defined as ‘such Things or Quantities as are supposed to be given or known, in order thereby to find out Things or Quantities which are unknown and sought for’.⁶ Ephraim Chambers in his Cyclopædia or, An universal dictionary of arts and sciences (1743) exemplifies such a generalized understanding in his entry on ‘Data’:

From the primary Use of the Word Data in Mathematicks, it has been transplanted into other Arts; as Philosophy, Medicine, &c where it expresses any Quantity, which, for the Sake of a present Calculation, is taken for granted to be such, without requiring an immediate Proof for its Certainty; called also the given Quantity, Number, or Power: and such things as are known; from whence either in Natural Philosophy, the animal Mechanism, or the Operation of Medicines, we come to the Knowledge of things before unknown, are now frequently in Physical Writers call’d Data.⁷

Against the backdrop of an early modern appreciation of Euclid, talk of data in this period often begins within the context of mathematical problem solving.⁸ ‘Data’ originally referred to what was given in a geometric proof.⁹ However, the Transactions corpus differs from other publications in certain foreseeable respects. For one, an early usage of ‘data’ in religious texts to refer to scriptural statements (‘given by God and therefore not susceptible to questioning’, as Daniel Rosenberg notes) is absent here.¹⁰ The latter point can be explained by the journal’s orientation toward natural philosophy, or, as the Society’s first secretary Henry Oldenburg puts it, its aim of ‘promoting the improvement of Philosophical Matters’ and ‘the communicating to such, as apply their Studies and Endeavours that way, such things as are discovered or put in practise by others’.¹¹ History too, which Rosenberg marks out as prominent in early usages of ‘data’, only has a marginal presence on these pages.¹² Still, what all this suggests is that debates in the fields of mathematics are instrumental for uses of ‘data’ to figure in the journal of the Royal Society.

How, if at all, does the picture of occurrences of ‘data’ change when considering the final quarter of the journal’s publications? Use of ‘data’ expands from its early origins in mathematics to many other fields, including empirically oriented ones. The final quarter of the publication (1831–1886) gives some clues about how this proceeds. Within this quarter, there are a total of 1401 documents published in the Philosophical Transactions. A search results in 1060 occurrences of ‘data’ in Q4, distributed over 386 documents (or hits in 27.55% of the total number of documents). Of these, only one single hit contains a participle use of ‘data’, and this is in a quotation from a Latin text published nearly a century earlier.¹³ All others use ‘data’ as a substantive.

When English became the main language of publication in the journal, was there any particular vernacular term that replaced the Latin ‘data’? This question arises especially for the field of mathematics, in which—some exceptions aside—the use of ‘data’ largely dries up after the 1760s. There is good reason to think that in English publications in mathematics the term ‘given’ takes on a role similar to the one ‘data’ once fulfilled in Latin.

Contemporary translations of Euclid—whose work had, after all, inspired much of the initial scientific use of the notion of data—show this usage. For example, Isaac Barrow renders the Latin ‘In data recta terminata triangulum aequilaterum construere’ (Elements, book 1, proposition 1) as ‘Upon a finite right line given AB, to describe an equilateral triangle ACB’, while John Keill puts it as: ‘To describe an Equilateral Triangle upon a given finite Right Line.’¹⁴ Similar examples can be found throughout early English translations of Euclid’s work. Mathematics publications in the Philosophical Transactions itself equally employ ‘given’ where the Latin would probably have used ‘data’. This goes beyond Bayes’ adaptation of the Euclidian data–quaesita formula (‘Given the number … Required the chance …’¹⁵) and occurs frequently in the adjectival use identified earlier, where authors refer to points, lines, angles or other mathematical quantities as given. For instance, already in 1668, James Gregory discusses how to ‘divide an Angle in a given ratio’. In 1735 the journal prints a Latin text full of references to ‘puncta data’ and ‘positione datae’, but adds the English title ‘A general method of describing curves, by the intersection of right-lines, moving about points in a given plane …’, again using ‘given’ for the Latin ‘data’. Even in his 1871 work on the mathematics of streams, William John Macquorn Rankine refers to a ‘given point’, ‘given proportion’, ‘given parameter’ or ‘given stream-line’ throughout.¹⁶ Hence, if any term replaced the Latin ‘data’ in vernacular mathematics publications, ‘given’ is a likely candidate.

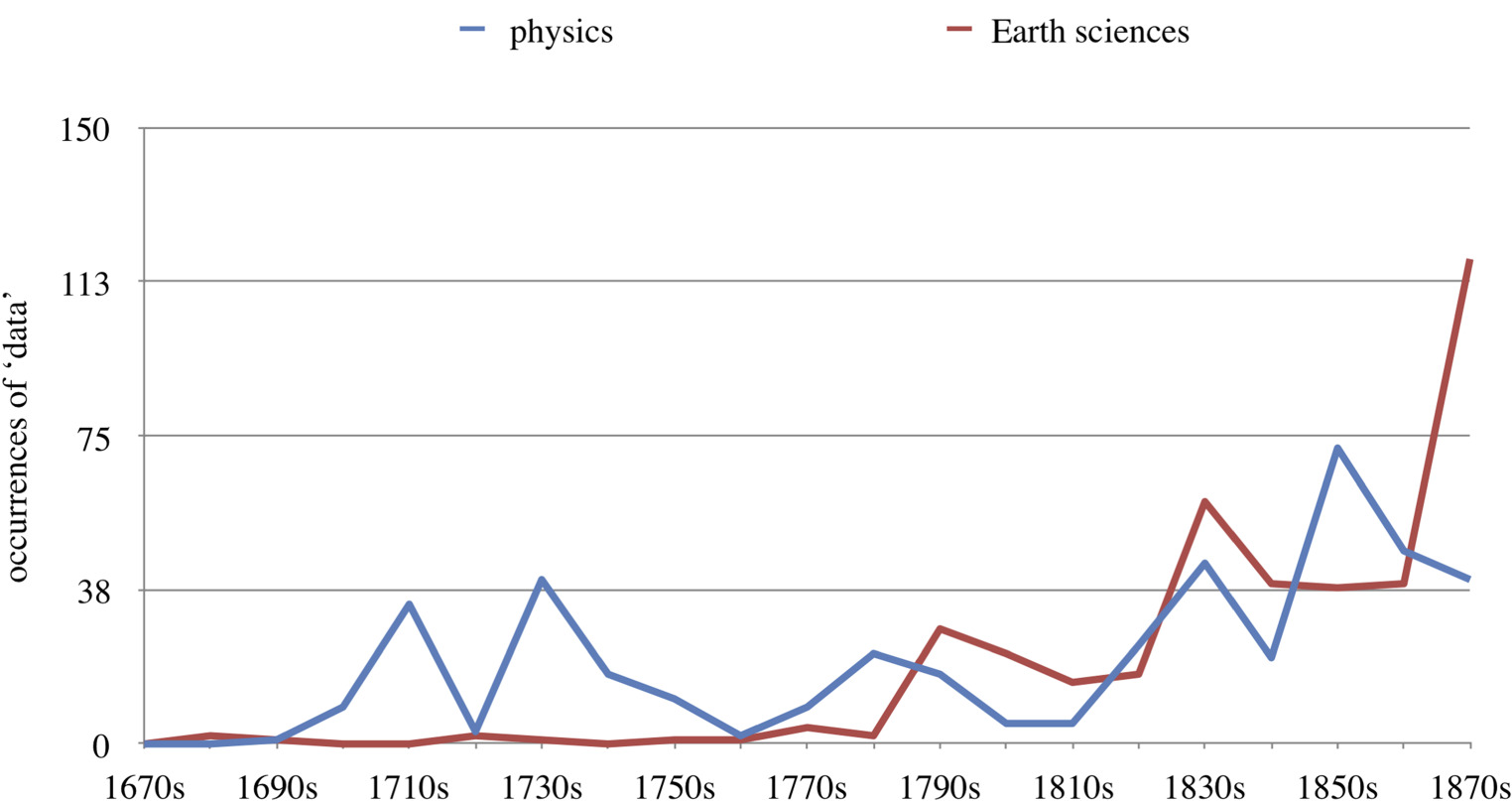
Returning to a broader assessment of the use of the term ‘data’ in various scientific fields, I found that 28.96% (307 hits) belonged to the category of Earth sciences, with another 28.96% (267 hits) in physics and a further 24.15% (256 hits) in chemistry. Biology follows as a good fourth, with 10.09% (107 hits). Figure 6 shows the distribution over time for the two top fields. In the area of Earth sciences, for example, in the late eighteenth going into the nineteenth century, one finds expanding studies published on conducted land surveys. For instance, when introducing a table of the degrees of longitude and latitude for France and the south of England, William Roy, who conducted multiple triangulation land surveys of Great Britain, states:

Now, although it is believed, that this table will be found to answer nearly in that zone of the earth for which it is intended; yet it is only offered for temporary use, until future observations … shall have furnished data for one more correct[ly].¹⁷

To accurately map zones of the Earth, more data points are needed to determine the mapping with ever greater precision.

In chemistry we can equally find discussion of data, in particular for tables with the results of experimental measurements, or overviews of chemical solutions. Here is an example by Heinrich Debus: ‘According to Noble and Abel, the chemical metamorphosis of gunpowder during explosion is a very complicated process, which cannot be explained with the data at their disposal.’¹⁸ Debus here uses ‘data’ to refer to the contents of a table with different compositions of chemical solutions for the use of gunpowder, and conceives of data within the framework of determining an explanation.

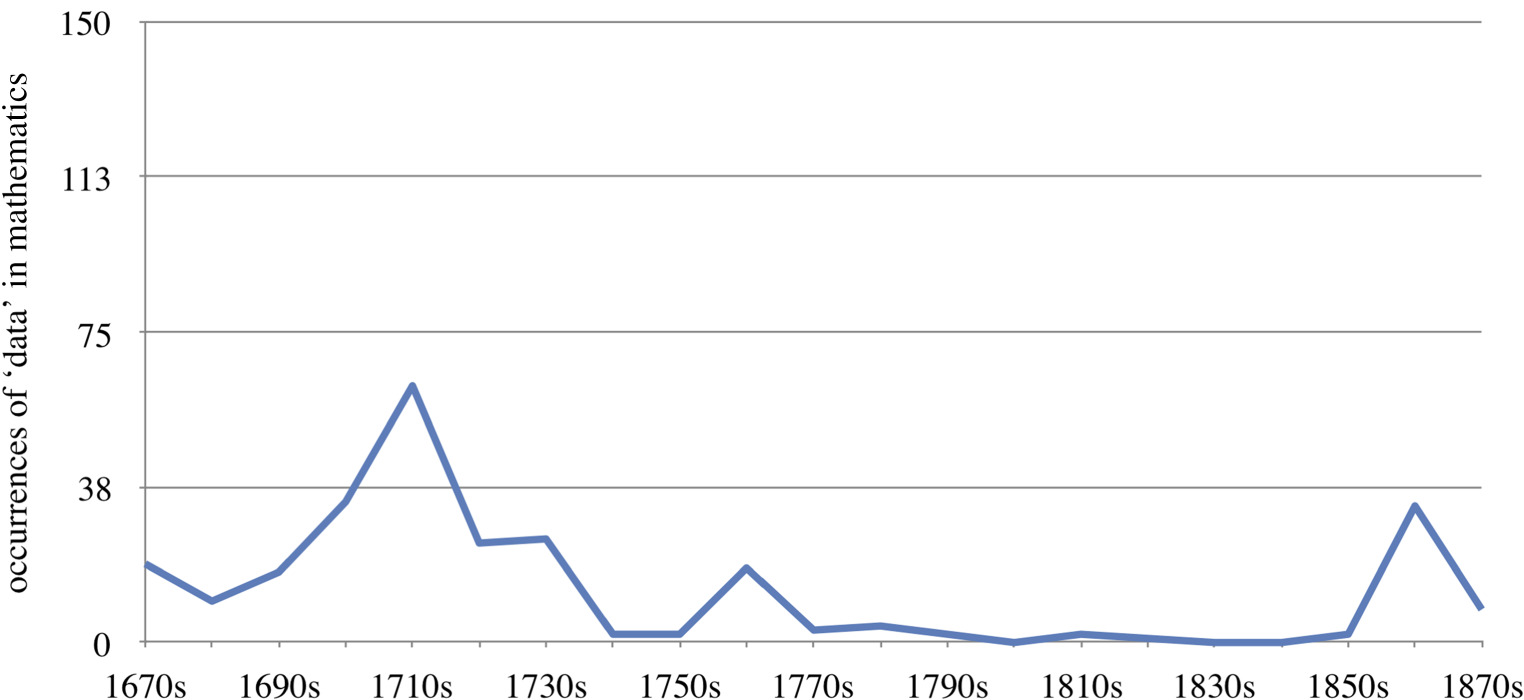
While data talk becomes increasingly common in Earth sciences, physics, chemistry and biology, in mathematics, on the other hand—once by far the largest field for discussions of data in the Transactions—its use is waning. In Q4 only 43 cases of use of ‘data’ occurred in this field. Figure 7 gives an overview of the development. This chart brings out the decline of the use of ‘data’ in the field of mathematics. We see occurrences of ‘data’ in mathematical documents from the earliest Transactions issues (a first hit in 1668) and with some regularity in the following decades, but a steady decrease is already visible from the mid eighteenth century and persists (with some exceptions) throughout the nineteenth. While in Q4 mathematics is certainly not the smallest field, it is far removed from the dominance it exhibited in Q1 of the journal’s publication.

These observations allow a further conclusion about how the use of ‘data’ develops within printed Royal Society documents. Whereas data talk gets introduced mainly through the field of mathematics, by the final quarter of the journal two things have happened. First, the word ‘data’ has moved away from its use as a participle in mainly Latin phrases, and instead has firmly established itself as a substantive, technical term. Further, this establishment of a technical notion of data was due most significantly to an uptake of data talk in three main fields, namely Earth sciences, physics and chemistry.

Some studies have suggested that the notion of ‘data’ itself undergoes a semantic ‘shift’ somewhere between the eighteenth and nineteenth centuries. However, authors differ in what exactly they take this shift to consist in. Rosenberg has located the shift in an altered functional role for data in argumentation. He suggests that ‘data’ initially functions to capture a premise or starting point in an argument (given its use in mainly a priori fields of inquiry, specifically mathematics) and then shifts to capturing the result of an argument or investigation (that is, when used predominantly in empirical studies).¹⁹ Furner identifies this change not so much as a shift from one argumentative function to another, but as a broadening of the notion of data based on its expanded usage. From an original geometric usage, he notes, by the start of the eighteenth century ‘data’ comes to refer to any mathematical quantities.²⁰ The basic claim that the notion of ‘data’ broadens in meaning appears well supported, and is at least consistent with the patterns found in the Philosophical Transactions; and, as I will lay out in what follows, we can push this point even further, to suggest that ‘data’ over the course of these centuries comes to be used even for cases that go beyond the giving and finding of quantities.

The many functions of data

How does use of the notion of data function within the various discussions of the Transactions? One obvious function, already discussed here, is the strict, original data-quaesita use within mathematics. In mathematical discussions appeal to data amounts to appeal to a fixed (supposed) quantity, which forms the basis for determining other quantities. As Chambers puts it:

Things given, a Term used in Mathematicks, Philosophy, &c implying certain Things, or Quantities supposed to be given, or known, in Order, from them, to find out other Things or Quantities, which are unknown, or sought for …²¹

Chambers defines data as functioning specifically within the context of mathematical problem solving. The usage is common for the data talk in mathematics, without much variation. However, this is certainly not the only way in which data figures in the Philosophical Transactions. In particular, when focusing on the cases where ‘data’ is used as a substantive, technical notion, more variation can be distinguished. I coded all 1396 cases of substantive uses of data for how they function, based on an assessment of the context of occurrence.²² In the range of results I ended up with, three major categories stood out: (I) data in computation; (II) data as information (observation, measurement); (III) data for theory. I will discuss these in turn.

Computing data

Frequently, data is used in, or as the basis of, processes of computation or calculation (I found 362 instances, or 25.93%, of the total of substantive uses of data). Given the roots of talk of data within mathematics and in astronomical calculations, it need not be surprising that discussion of data often arises in the context of computing or finding quantities. And indeed, also beyond the extensive range of cases of ‘data’ used as a participle, there are some instances in the later corpus where ideas about data and those of mathematics coincide. For example, when discussing probabilities, George Boole states:

Principle II.—When the data have been translated into probabilities of events connected by conditions logical in form and explicitly known, the problem may be constructed from a scheme of corresponding ideal events which are free, and of which the probabilities are such that when they (the ideal events) are restricted by the same conditions as the events in the data, their calculated probabilities will become the same as the given probabilities of the events in the data.²³

Data for Boole here are events that enable the calculation of probabilities, which are numerical. With those probabilities in hand, one can make calculations to find yet further chances of events.

However, it turns out that discussions about calculating data are not at all restricted to the fields of mathematics. In fact, in my examination I found an even stronger correlation (code co-occurrence) between references to data and computation within other fields. There is a reasonable correlation between this mathematical use of ‘data’ and the domains of Earth sciences (correlation coefficient 0.15), physics (correlation 0.15) and to a certain extent also astronomy (0.07). Some examples can bring out how calculating data is entrenched in these fields. For instance, in determining ratios between Martian and terrestrial gravity, an author may write ‘The data for the calculation are …’²⁴, and proceed to compute these data. Elsewhere, drawing on pre-existing records: ‘This calculation is founded on data supplied by M. Agassiz in his “Système Glaciaire”.’²⁵ In an 1855 communication on geodesy in the Himalaya regions, John Henry Pratt states:

The complete application of the method I have developed requires a full survey of the earth’s superficies. In the absence, however, of sufficiently accurate and extensive information to make an exact calculation, I propose now to use such data as I have been able to gather—chiefly from books on geography and Humboldt’s works, as well as the published Maps of the Indian Survey—to obtain an approximation to the amount of attraction on the plumb-line on the Indian arc.²⁶

In an article responding to Michael Faraday’s work on electromagnetism, an author indicates how they have acquired new data to perform a more accurate calculation:

In the Preliminary Note the reducing factor for this tube was given as −99449. The alteration is due to the use of more precise data in place of some quite rough measurements in round numbers on which, by an oversight, the first calculation was founded.²⁷

This shows that ideas about data as the basis for computation have gained extensive presence outside of their original fields of mathematics, namely also in Earth sciences and physics. This suggests two things. First, that there is a continuity in at least certain aspects of the original usage of data, in that the idea that data have a role in computation is still salient. Second, it also indicates an expansion in terms of the sorts of things that can figure as data. The range of things that one can have as given has extended beyond the realm of pure points and lines, and has come to incorporate more general observations and measurements (though these will often still be expressed numerically).

Data as information

Another function, and by far the largest (I found 470 cases), is where ‘data’ is used to designate simply the availability of a piece of information. In these cases, when authors speak of ‘data’, it could quite naturally substitute for any of a range of other epistemic units, such as observations, measurements or even information itself. Such a more general function of ‘data’ is in line with a suggestion in the literature that, especially in certain early modern discussions (Kepler and Priestley come up, among others), ‘data’ tends to refer to experimental measurements, or what is given in experience, and that ‘phenomena’, ‘observations’ or ‘effects’ may have been used just as well.²⁸ Müller-Wille suggests that ‘data’ was long used to refer to any kind of information.²⁹

In fact, for the Royal Society corpus, I found that occurrences of ‘observation’, ‘phenomena’ (phaenomena), ‘measurement’ and ‘fact’ were actually more likely in documents that also use ‘data’ than in other documents of the corpus.³⁰ (For ‘information’, itself a newly developing notion in the early modern period, I found no such correlation.) This suggests that in certain cases these terms are likely to occur in the same discourses. One way to understand correlations like these is by acknowledging the far wider rise of practices of (what we can call) data gathering and quantitative methods in the background.³¹ Sabina Leonelli has emphasized that, for big data today, ‘[t]here is strong continuity with practices of large data collection and assemblage conducted since the early modern period’.³² Looking more generally within the Philosophical Transactions at uses of ‘data’ as denoting pieces of information, there was a particularly strong correlation between this quite generic use and the fields of Earth sciences (correlation coefficient 0.26), as well as biology (0.12) and physics (0.11) and to a certain extent astronomy (0.06). Let me take the case of Earth sciences as an example.

In the late eighteenth and well into the nineteenth century, Earth science saw a flurry of activity with the production of trigonometric surveys, conducted to determine the distances and angles between terrestrial points. This included the Ordnance Survey of Great Britain (started 1784) led by William Roy, and the Great Trigonometrical Survey in India (started 1802). As part of such projects of surveying, scientists gathered masses of observational data, of which records were frequently communicated on the pages of the Transactions. When Roy speaks of ‘future observations … shall have furnished data’,³³ he uses ‘data’ as more or less equivalent to ‘observation’. Other documents provide table upon table, elaborating in each case what can be determined based on the data represented. Here is another: ‘In all cases in which the data were equally correct, no doubt the direction of meridians might be computed, without fear of the results deviating much from the truth.’³⁴ Authors in these projects seem to conceive of their recordings as ‘data’, givens, which would enable them to arrive at missing or more accurate quantities.

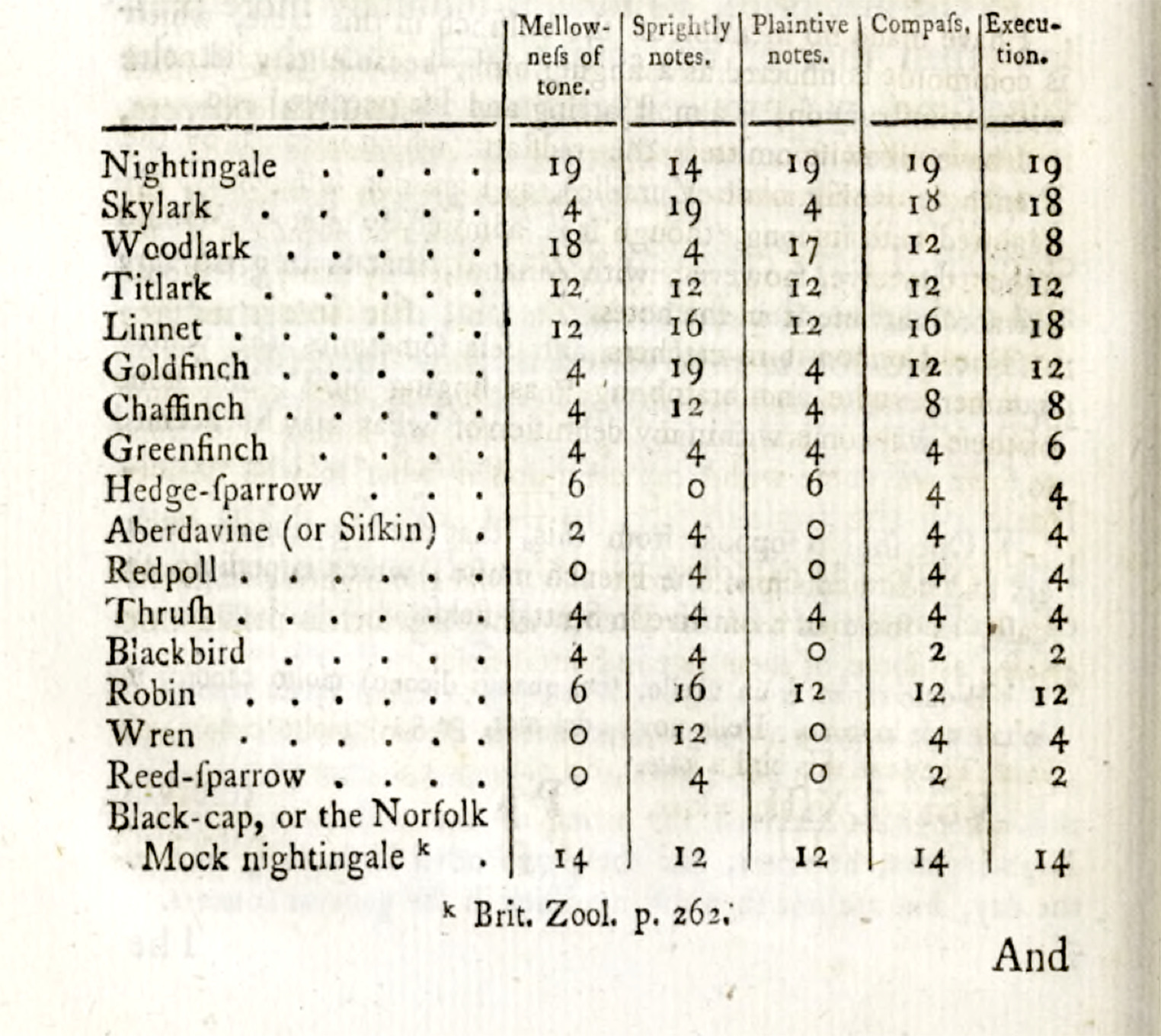
Practices of data gathering crop up not just in the use of statistics, but also in data visualization, including the increasing use of tables, graphs and timelines.³⁵ Precisely such practices of data (or: information, observation, measurement) gathering, even when they are not labelled as such, show up in the Philosophical Transactions during the period studied here with increasing frequency. An early example of the use of tables that coincides with a discussion of data is in a text by lawyer and naturalist Daines Barrington, then Vice-President of the Society, comparing the capacities for song in different birds. He notes that:

The following notes, therefore, having been observed in different birds, viz. A. B. flat, C. D. F. and G. the E. is only wanting to compleat the scale; the six other notes, however, afford sufficient data for making some conjectures, at least, with regard to the key in which birds maybe supposed to sing.³⁶

These ‘data’, combined with further observations about bird song, bring Barrington subsequently to compile a table with a quantitative assessment of the comparative merits of birds’ song capacities, as shown in figure 8. This is one way in which ‘data’ functions to refer to pieces of information more generally.

The use of printed tables to present data or information—including logarithmic tables, tables for use in navigation, astronomical tables, tables for use in trigonometry—shows a marked increase over time on the pages of the Royal Society journal. Looking just at the subset of documents in which there is already some mention of data, I found that many of those also include one or more tables. The portion of documents with tables within this subset increases from a yearly average of only 0.3% in Q1, to 21.89% in Q4, with a most notable increase from ca 1790 onwards. These practices of data gathering and data visualization show that the term ‘data’ may on occasion be used interchangeably with terms such as ‘observations’ or ‘measurements’ as designating bits of information.

Data and theory

A third function of data that I found centres around the relation between data and theory. Authors publishing in the Philosophical Transactions regularly suggest that data in some way relate to theory. For example, we find authors discussing how data will help them found a theory. Discussing the Leiden physician Boerhaave’s views on animal physiology, one writes:

Such was Boerhaave’s doctrine concerning the vascular system of animal bodies; like many of his other notions, ingenious, plausible, and recommending itself, at first sight, by an appearance of geometrical and mechanical accuracy: but founded upon insufficient data, and by no means to be reconciled to appearances.³⁷

Others note that they are still in need of ‘obtaining numerical results as data for the foundation of a theory’³⁸, or that they need to make certain calculations ‘to furnish data for the future construction of a philosophical theory’.³⁹ Elsewhere an author rebukes philosophers for drawing inferences from insufficient data: ‘It would be useless to enumerate the labours of those philosophers, who in following, or varying from the steps of Galileo, have merely tended to obscure a subject respecting which they had no data to proceed upon.’⁴⁰ We also find claims about how data may test, verify or refute a theory. For example, one author notes that ‘the data from which a semiconjugate is computed … must be admitted to be highly favourable to the Huygenian theory’.⁴¹ Another notes: ‘Sufficient data were not at the command of either of the authorities we have named to enable them adequately to test their theories.’⁴² And yet elsewhere we find someone claiming: ‘We are now furnished with data to verify, or refute it.’⁴³ Some in the literature have elaborated how data or other epistemic units were understood to relate to theory. Wootton, focusing on facts, speaks about the Renaissance as identifying the existence of ‘killer facts’ that can completely undermine a theory.⁴⁴ Both Poovey and Fontes Da Costa have suggested that in Baconian circles, facts came to be understood as theory-neutral or, as Poovey puts it, as a ‘nugget of experience detached from theory’.⁴⁵ Could this be data’s role in relation to theory too? Bogen and Woodward suggest that any relation between data and theory proceeds through phenomena: data are evidence for the existence of phenomena, and theories should aim to explain not data, but phenomena (or facts about phenomena).⁴⁶

There is a case for considering also these more extended usages still as an expansion of the original data–quaesita structure, where one thing is held as fixed in order to determine another. This works as follows. Originally, on the mathematical use of data, one would have quantity X given and another quantity Y sought. One expansion at work shows up in how a broader set of things can be either given or sought—not just ratios or angles. Where ‘data’ is used to refer to information, I found that also observations, measurements or information more generally could function as a data or quaesita. The discussion of the relation between data and theory suggests a further expansion, where data can even help determine something different in kind, namely a theory.

The idea that data are indeed conceived of as a different kind of thing from theory would seem to be held by at least one of the authors publishing in the Transactions, who writes:

I contented myself with ascertaining, first, the proportions of saline matter yielded by a given quantity of each water, and afterwards, the proportions of acids and earths contained in these respective waters; thus presenting data which are quite divested of theoretical views, and from which the composition of those waters may at any time be inferred in the way which may be deemed most eligible.⁴⁷

If data are ‘quite divested of theoretical views’, then data and theoretical views cannot be the same thing. Hence, if my diagnosis is correct, here is at least one example of how data on this expanded conception could help determine something of a quite different kind.

Data’s epistemic structure

There is indication that within the early Royal Society Transactions corpus, talk of data retains an epistemic structure. It picks out that which is held fixed (the datum), while something else is being sought (the quaesitum). In the early decades of the Society’s publication, when talk of data enters through the field of mathematics, both the nature of whatever can occupy the places of what was given or sought, as well as the relation between those two elements, were highly restricted. Both the sought and found were quantities, and the relation of the one to the other was one of determination (calculation). Over the decades, as use of ‘data’ in mathematics persists, and even grows in other empirically oriented fields—including Earth sciences, physics, chemistry and biology—the epistemic structure associated with data loosens up. In the place of what is given and sought are not just quantities but also more generally observations, experimental results, measurements or, as shown above, even theories. From a relation initially between things of the same kind (say, quantities), it now may also relate two things of completely different kinds (say, observations and doctrines). Moreover, the relation between the data to the quaesita also allows for an extended range of options. Depending on the particular discussion, one’s data may still determine a required quantity, but it may also determine (be the foundation of) or confirm or deny a hypothesis. That is, the precise epistemic relation gets broadened (dispersed) from not only one of derivation to also one of support, verification and other options.

One might question whether this proposed epistemic structure for data is really found in this corpus. For one thing, some authors equally suggest, seemingly contradictorily, that data might also not be given. Commenting on a table that lists stress differences of various materials, George Darwin complains: ‘Rankine does not give the data for this quantity.’⁴⁸ This suggests that not all data are actually data. Furthermore, authors in the Transactions regularly comment on how their data is precisely not to be held fixed or assumed, because it turns out to be erroneous, inaccurate on unreliable. Here is Charles Wheatstone:

Immediately after the publication of Chladni’s experiments on square plates, James Bernouilli attempted to demonstrate them analytically; but his investigation was entirely unsuccessful; his conclusions were founded on erroneous data, and the results he obtained were at variance with experiment.⁴⁹

On a case of measuring angles with faulty instruments, James Short complains: ‘The error of the instrument becomes itself one of the data.’⁵⁰ If data can fail to be given, or can be erroneous, in what sense are they something that are held fixed while other things—quantities, numbers, phenomena, theories—are sought?

However, precisely these cases where data are not given, or are in some way to be set aside as erroneous, can support the claim about data as implying an epistemic structure, be it from an unexpected angle. Error is unproblematic because, as was noted earlier, being a datum (being given) does not itself come with any implication of knowledge or truth. Data themselves are not alethic in this sense. What makes something a datum is that it has the status of something provided in a process of problem solving or investigation. That data can also fail to be given can indirectly lend support to the idea that data’s being available was precisely what was expected. When in the hypothesized epistemic structure the place of the fixed quantity (or: observation, measurement) goes unoccupied, this may get flagged. That where one would expect something given can turn out to be empty shows that it is this structural role, not the particular piece of information, which is most strongly associated with data in these discussions.

This diagnosis, that the concept of data in the discussions of the Royal Society comes with an associated epistemic structure, might be thought to resemble what in the literature has been called an ‘evidential interpretation’ of data.⁵¹ On the evidential interpretation, data can function as evidence for theories or hypotheses. However, despite similarities, for uses of ‘data’ in the Royal Society documents, the category of evidence appears too narrow. Evidence is what one can have for, say, theories, hypotheses or the existence of phenomena. It is not an adequate category for describing the early mathematical uses of data. In the mathematical context, if one ratio is given and another sought, the former ratio would not normally be understood as evidence for the other. Rather, it is simply the basis for determining the other ratio. It would therefore be misleading to call the original mathematical data–quaesita structure an evidential relation. By contrast, the epistemic structure proposed here is not so narrow. As shown, when the notion of data expanded from an original occurrence in mathematics, it incorporated the possibility of data functioning as evidence. But it is not restricted to such inductive use. As indicated, the epistemic structure can equally be filled out as one of a priori determination or of verification. Hence, for the Royal Society publication, the diagnosis that the concept of data comes with an epistemic structure is more accurate than the evidential interpretation.

Conclusion

The notion of ‘data’ occurs in the Royal Society’s Philosophical Transactions in a plurality of ways. Apart from verbal uses (data as giving), or indications of a date (meta-data), it also figures as a substantive to indicate a technical notion of something being ‘given’. Focusing on those substantive uses, here I have argued that in those cases the concept comes with a certain implied epistemic structure: data are those things held fixed, while one seeks to determine other things. Working from a study of basic trends and divisions in how ‘data’ occurs in the Society’s publications, I have shown how this structure starts out in debates in mathematics with a very specific implementation—where both what is given and what is sought are quantities, and one would move from the one to the other through determination or calculation—through an expansion of data talk into other, empirically oriented fields (including Earth sciences, physics and chemistry). Also, the concept of data expands, admitting a wider range of things given (including observations, measurements, information) as well as sought (including things of a different kind, such as theories). This study provides an initial account of how ‘data’ was understood in the works of a particular learned society prior to the big data revolution.

Acknowledgements

Work for this article was in part carried out while I was a visiting fellow at the Center for Philosophy of Science, University of Pittsburgh. I thank the Center for offering such a welcoming environment and my then-colleagues Edouard Machery, Colin Allen, Karen Kovaka, James Fraser, Ulrich Gähde, Vincenzo Fano, James Justus and Armin Schulz for discussion.